Differentially Private Hypothesis Tests and Change Point Estimation through Edit Distance

Supervisors: Adam Groce , Andrew Bray
Collaborators: Zachary Barbanell , Wolfgang Brightenburg , Kellen Brosnahan , Daniel Zou

Overview

Differential Privacy is a mathematical definition for analyzing the privacy preservation. Basic anonymization techniques such as removing names from databases have repeatedly been shown to be ineffective, as it is possible to re-identify individuals by linking their data to other publicly available data. Differential privacy guarantees that the result of a query (such as a hypothesis test) reveals almost nothing about any single individual in the dataset. Differentially private hypothesis tests allows researchers to conduct statistical analysis while truly protecting the privacy of research participants. Our goal is to reduce the accuracy cost of private hypothesis tests.

While public hypothesis testing often calculates a test statistic and compares its value a threshold to compute a p-value, differentially private hypothesis testing utilizes a different approach. We use the Laplace Mechanism to add noise to the statistic value, and then compare the noisy statistic value to the threshold to compute a noisy p-value. We then use the noisy p-value to determine whether to reject or accept the null hypothesis.

The noise is proportional to the sensitivity of the statistic, which is the maximum a statistic can change if we alter the data of a single individual. This ensures that the noise added is not too large, so that the noisy p-value is still accurate, but also not too small, so that the noisy p-value still preserves differential privacy.

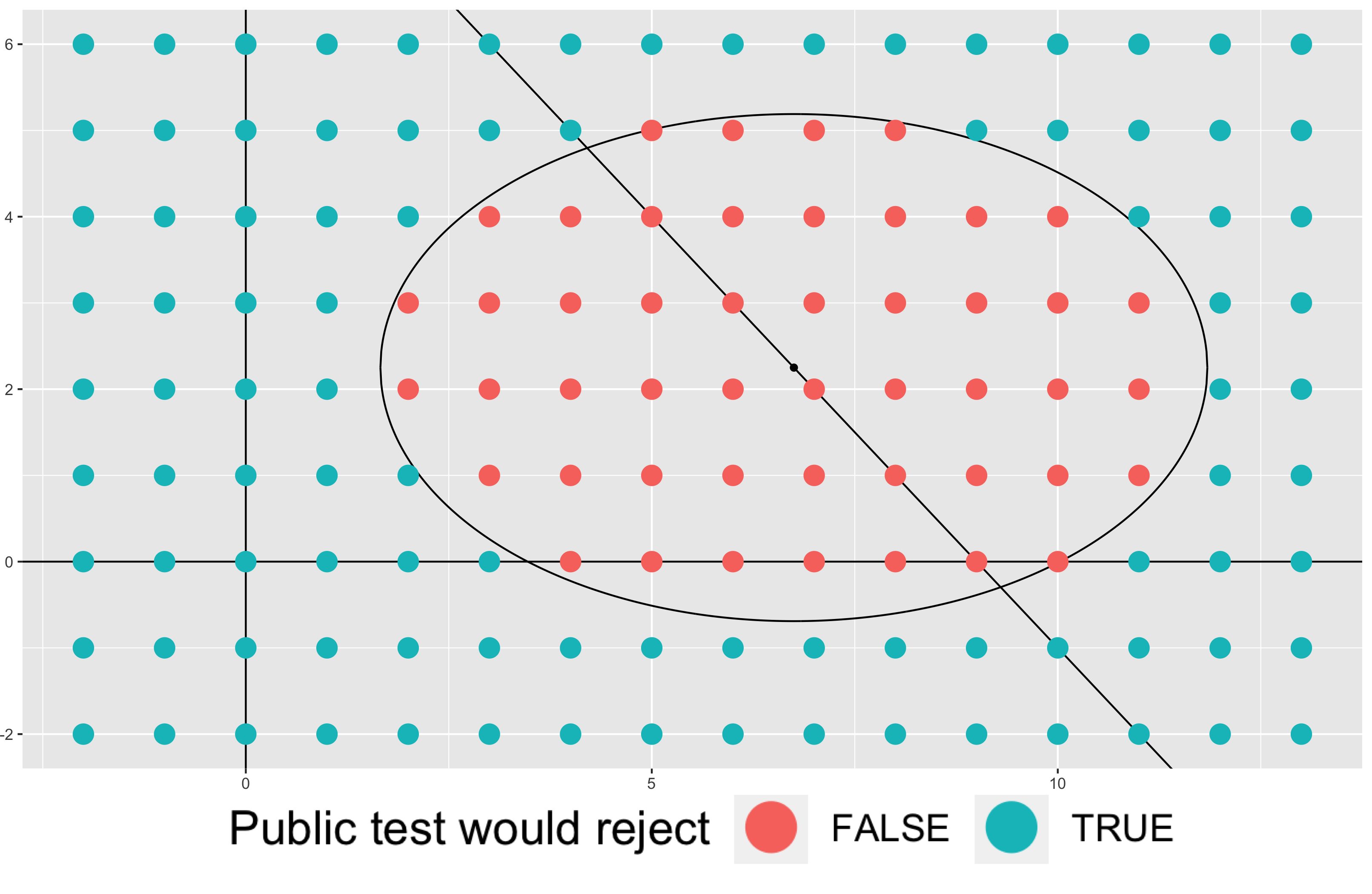
An edit is defined as a change of an individual’s data, and edit distance is the minimal number of edits necessary to enter (or leave) the rejection set of the public test. Edit distance itself as a test statistic has low and constant sensitivity, so less noise is added by the Laplace Mechanism, making the noisy statistic more accurate. Using edit distance as a test statistic is our main contribution, and we present edit distance tests in four different settings.

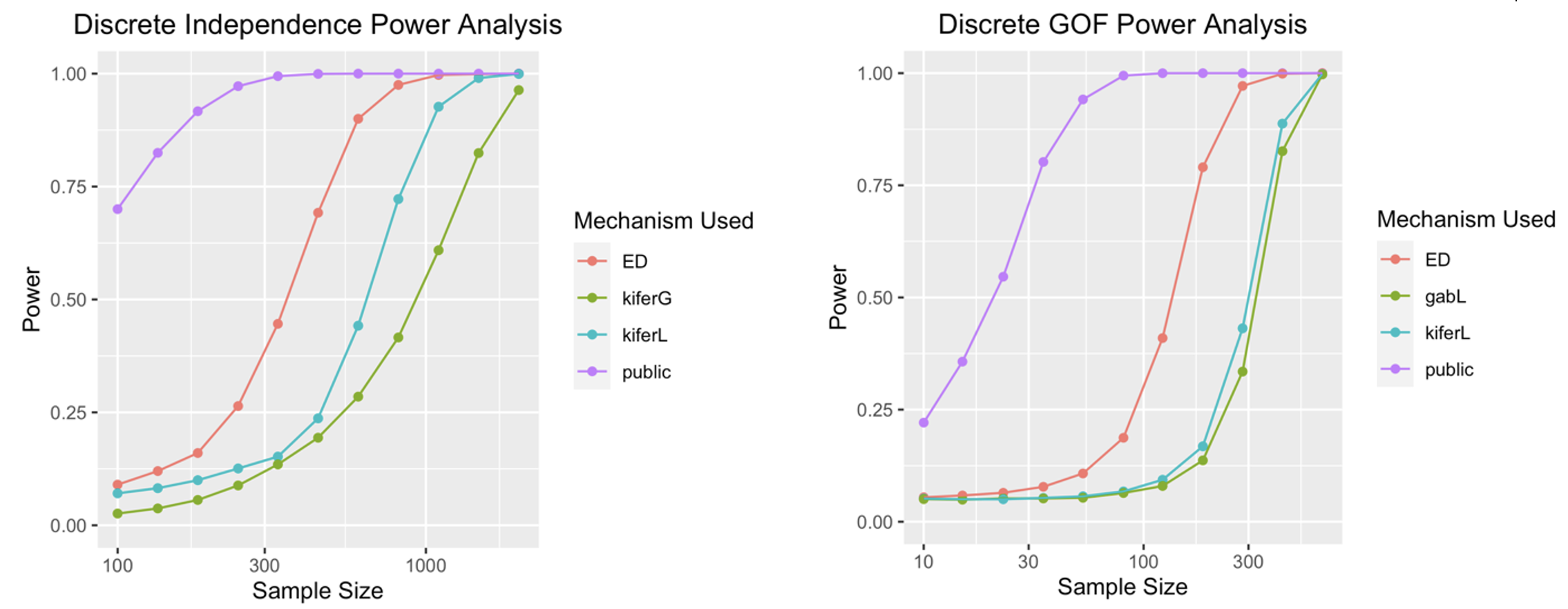
1. For Goodness of Fit, we have a single categorical variable and its expected distribution. We want to know whether the data contradicts our expectations.
2. For Independence, we have 2 categorical variables in a contingency table. We want to know whether the variables are independent.

The public tests are chi-squared tests, and the state-of-the-art private tests are by Rogers and Kifer (Kifer & Rogers, 2016). It involves adding input noise, then computing an altered chi-squared stat. Other prior work includes Gaboardi et al. (Gaboardi et al., 2016) Our test computes edit distance to the public chi-squared threshold, then adds noise. As the figures above show, our edit distance method achieves a high power with a much lower sample size.

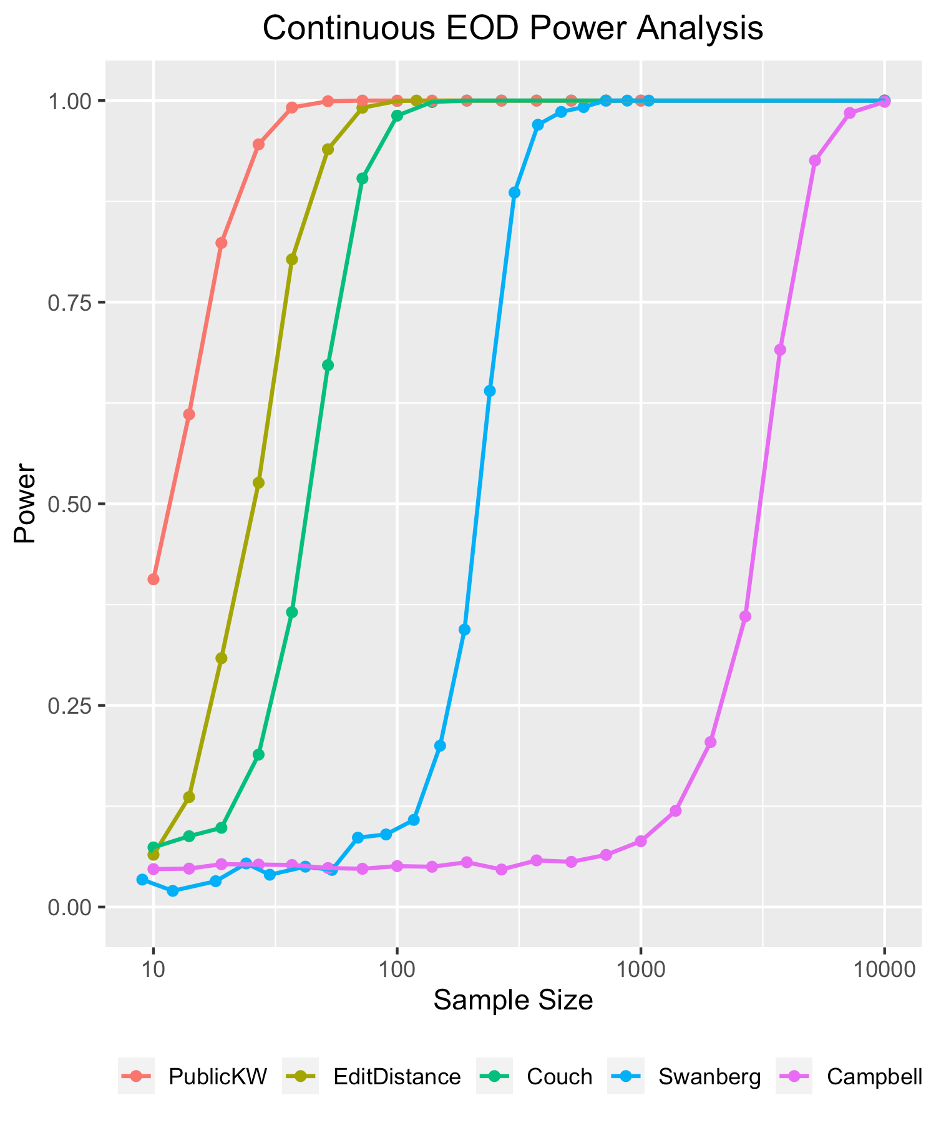
1. For Equality of Distribution, we have multiple groups and a continuous response variable. We wish to determine whether the different groups share the same distribution.

The state-of-the-art test for this setting, the Absolute Value Kruskal-Wallis test, was designed by a Reed group, Couch et al.Previous endeavors into this setting have also been done by Reed groups: Swanberg et al. (Swanberg et al., 2019) and Campbell et al. (Campbell et al., 2018) Our test measures the edit distance of a database to a set of databases with predetermined Absolute Value Kruskal-Wallis values. The right figure shows how we can achieve a high power with a lower sample size.

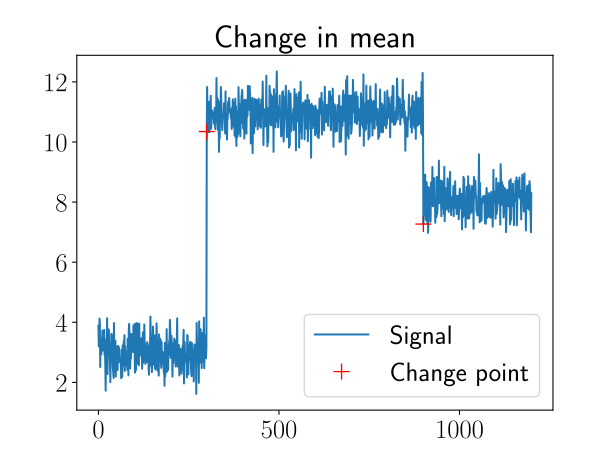
1. For Change Point Estimation, which is a slightly different setting from hypothesis testing, we have a time series of a single numeric variable whose distribution changed at an unknown point in time. We wish to estimate the position of the change.

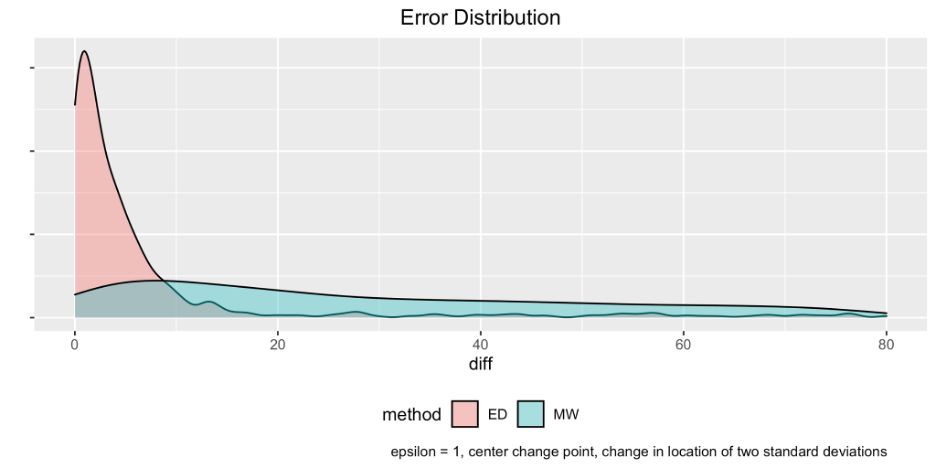
The previous state-of-the-art method uses the Mann-Whitney statistic, calculated at each candidate, added noise, and reporting the index of the minimum stat (Cummings et al., 2020). Our test computes edit distance to maximum Mann-Whitney statistic and calculates the statistics within windows instead of using the entire dataset, increasing accuracy and reducing bias in estimation. The figure below shows that our error distribution is more concentrated around 0, indicating that our test is more accurate.

Acknowledgement

This material is based upon work supported by the National Science Foundation under Grant No. SaTC-1817245.